معمای ریاضی تیزهوشان با جواب؛ ۳ معمای گیج کننده و چالشی

معماهای ریاضی همانند حل مکعب روبیک از جمله معماهای جذاب و بسیار سرگرم کننده هستند که گاهی هوش و ذکاوت افراد را به چالش می‌کشد. سوالات مطرح شده در این دسته (یعنی معمای ریاضی تیزهوشان) بسیار سخت هستند و می‌توانند ظرفیت ذهنی افراد را بالا برده و به نحوه تفکر درباره موضوعات سخت کمک نمایند. در ادامه به طرح چند معمای ریاضی تیزهوشان با جواب خواهیم پرداخت. با ما همراه باشید.

معمای پروفسور حسابی

سه نفر برای خرید یک ساعت به ساعت فروشی رفتند و قیمت یک ساعت را از شاگرد مغازه پرسیدند. ساعت سی هزار تومان بود و هر کدام نفری ده هزار تومان پرداخت کردند و ساعت را خریدند. همان موقع صاحب مغازه به شاگردش گفت قیمت ساعت بیست و پنچ هزار تومان بوده و پنج هزار تومان مبلغ اضافه را سریعا به آن‌ها برگردان. شاگرد مغازه دو هزار تومان را برای خود برداشت و سه هزار تومان باقیمانده را به آن‌ها پس داد (نفری هزار تومان).

به این صورت یعنی هر کدام از آن سه نفر، نه هزار تومان پرداخت کرده‌اند که می‌شود بیست و هفت هزار تومان. به علاوه دو هزارتومان شاگرد مغازه که می‌شود بیست و نه هزار تومان.

پس هزار تومان باقیمانده کجاست؟

پاسخ معما 👇

.
.
.
.

اشتباه همین جاست که نباید ۲۷ را با ۲ جمع کرد و در واقع باید آنها را از هم کم کرد.  یعنی سه نفر ۳۰ هزار تومان پول دادند که ۳ هزار تومان را شاگرد به آنها برگرداند.

پس آنها ۲۷ هزار تومان دادند که ۲ هزار تومان رو شاگرد برداشت و ۲۵ هزار تومان را بابت پول ساعت پرداخته اند.

معمای گیج کننده اعداد

فرض کنید ۵۰ هزار تومان پول داشته و می‌خواهید طی روزهای مختلف این پول را خرج کنید. خب مرحله به مرحله با هم جلو می‌رویم.

روز اول: در روز اول ما ۲۰ هزار تومان از پول رو خرج کردیم. چیزی که باقی می‌ماند۳۰ هزار تومان است.

روز دوم: از ۳۰ تومان باقی مانده ۱۵ هزار تومان را خرج می‌کنیم و ۱۵ هزار تومان دیگه برای ما باقی می‌ماند.

روز سوم: از ۱۵ هزار تومان باقی مانده ۹ هزار تومان خرید می‌کنیم و چیزی که در جیب‌مان باقی می‌ماند فقط ۶ هزار تومان است.

روز چهارم: هر مقداری که باقی است (۶ هزار تومان) را خرج می‌کنیم و دیگر عملا پولی نداریم.

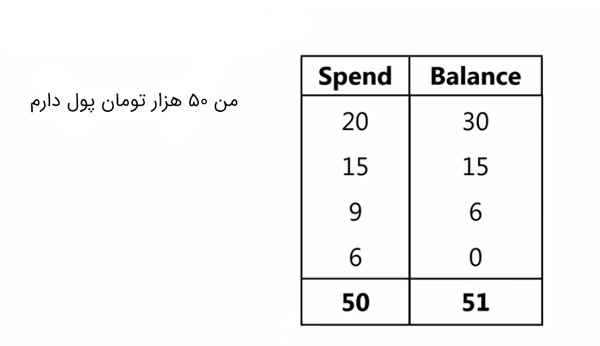
اما این معما چی رو از ما میخواد؟

مجموع پول‌های خرج شده ۵۰ هزار تومان است ولی مجموع پول‌های باقی مانده در روزهای مختلف ۵۱ هزار تومان است! این هزار تومان از کجا آمده؟؟؟

پاسخ معما 👇

.
.
.
.

خب حل این معما در نگاه اول به نظر خیلی سخت می‌آید ولی اینگونه نیست! در ادامه راه حل را به صورت تصویری و کاملا گویا بررسی خواهیم کرد.

روز اول:

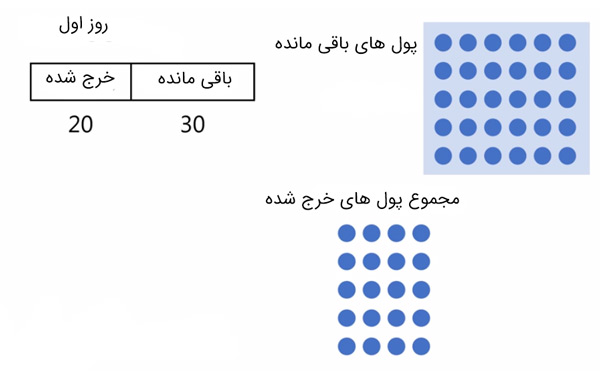
روز دوم:

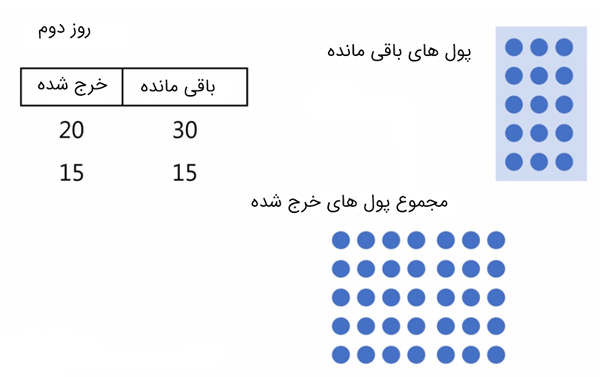
روز سوم:

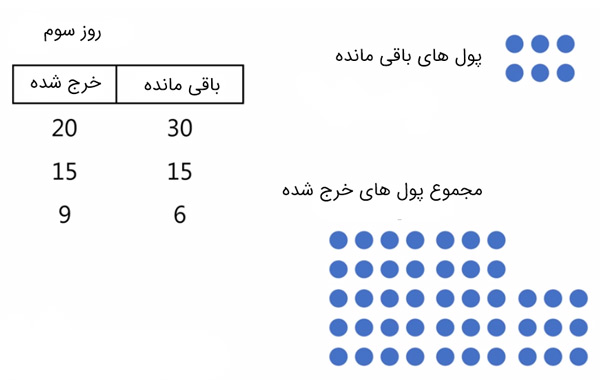
روز چهارم:

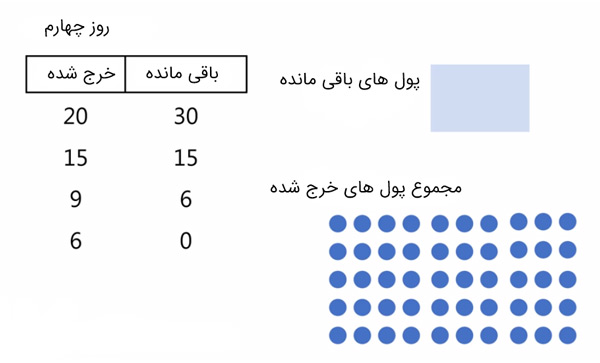
اما چرا در ظاهر جمع این دو ستون یکسان نیست؟

در واقع جمع این دو ستون اصلا ربطی به هم ندارن و هیچ مشکلی پیش نیامده. این فقط ترفند و حقه‌ای در ریاضی است تا شما فکر کنید این وسط هزار تومن بوجود آمده است. کافی است اعداد رو عوض کنید تا ببینید که اختلاف دو ستون خیلی بیشتر از هزار تومان می‌شود. پس این دو ربطی به هم ندارند.

معمای سقوط تخم‌مرغ از ساختمان

در ابتدا به شما دو عدد تخم‌مرغ داده می‌شود و سپس به بالای یک ساختمان ۱۰۰ طبقه می‌روید. تخم‌مرغ‌ها می‌توانند فوق‌العاده شکننده یا بی‌نهایت سخت باشند. به این معنی که یک تخم‌مرغ ممکن است با سقوط از اولین طبقه بشکند یا پس از سقوط از طبقه صدم هیچ آسیبی نبیند. علاوه بر این هر دو تخم‌مرغ، دقیقا شبیه به یکدیگر هستند. شما باید به این مسأله پی ببرید که: “بالاترین طبقه‌ای که تخم‌‌مرغ‌ با سقوط از آن نمی‌شکند کدام است.”

حال سؤال این است که شما به چند سقوط برای یافتن جواب این پرسش نیازمندید؟